Answer

For the table not to fall, the center of the circle must be inside the triangle formed by the three legs. To see why, imagine different setups: if the circle’s center is outside the triangle, all three legs end up on one side of the circle, and the table falls.

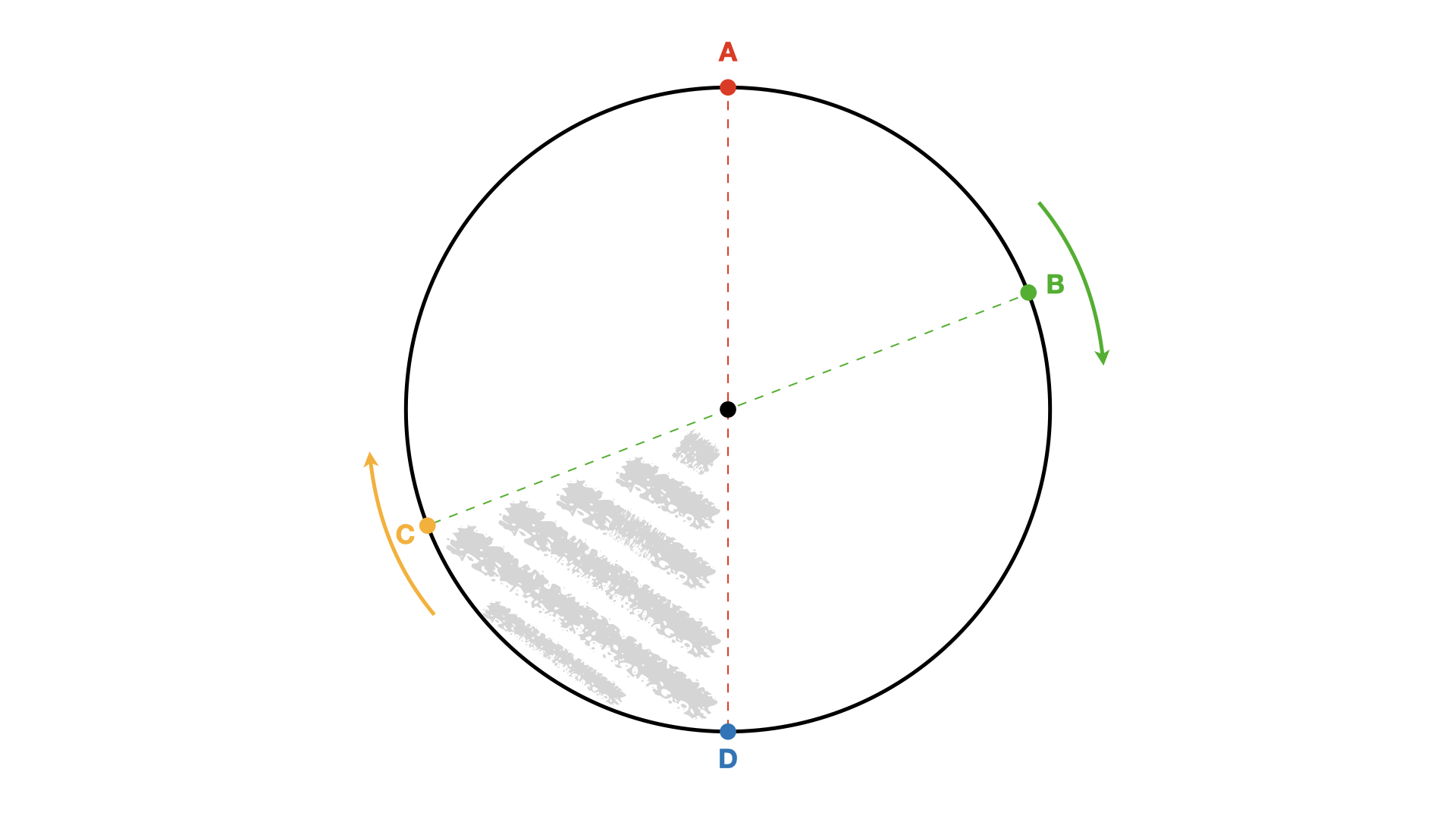
To solve this, we fix one leg and vary the position of the second leg to find where the third leg must go to keep the table stable. Fix the first leg at any point (call it A in the image below). Since the table is circular, the choice of A doesn’t matter. For the second leg, we only need to consider its position between points A and D. This is because the circle is symmetric, and placing the leg anywhere beyond D is like flipping the circle around the y-axis.

Now, once the second leg is placed, there is a specific area (the grey zone in the image) where the third leg can go without the table falling. Outside this area, all legs end up on one side of the circle, and the table falls. If the second leg is close to point A, the grey area is small. If it’s near point D, the grey area is almost half the circle. As the second leg moves randomly, the grey area ranges from 0 (when the second leg is at A) to 1/2 the circle (when the second leg is at D). On average, this safe zone is 1/4 of the circle. If the third leg is randomly placed around the circle, the chance it lands in the safe zone is 1/4.