Answer

On the first look, it's not immediately obvious what shape we'll get when the two cylinders intersect. Instead, let's break up the problem into manageable chunks. For instance, it's easier to visualise 2D intersections and sum them up instead of trying to imagine what the 3D intersection looks like. So we can view one of the cylinders as a stack of discs of radius 1, and consider the intersection volume as a sum of 2D intersections between the discs and the cylinder, as in the image below:

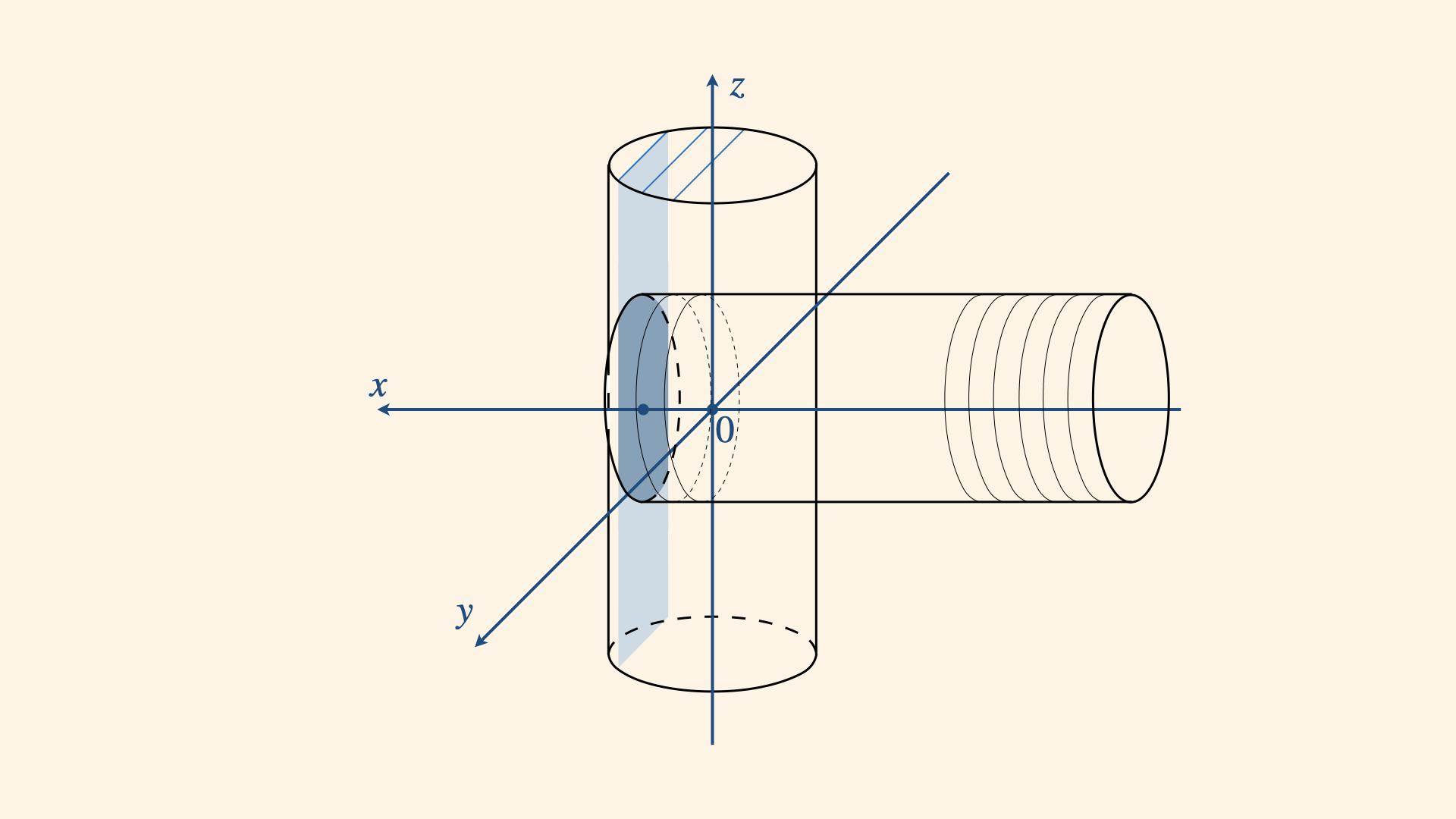To find the intersection volume, we can slice the cylinder with the disc going from $x=-1$ to $x=+1$, and sum the intersections (dark shaded blue). As we move from -1 to 1, the 2D intersections look as follows:

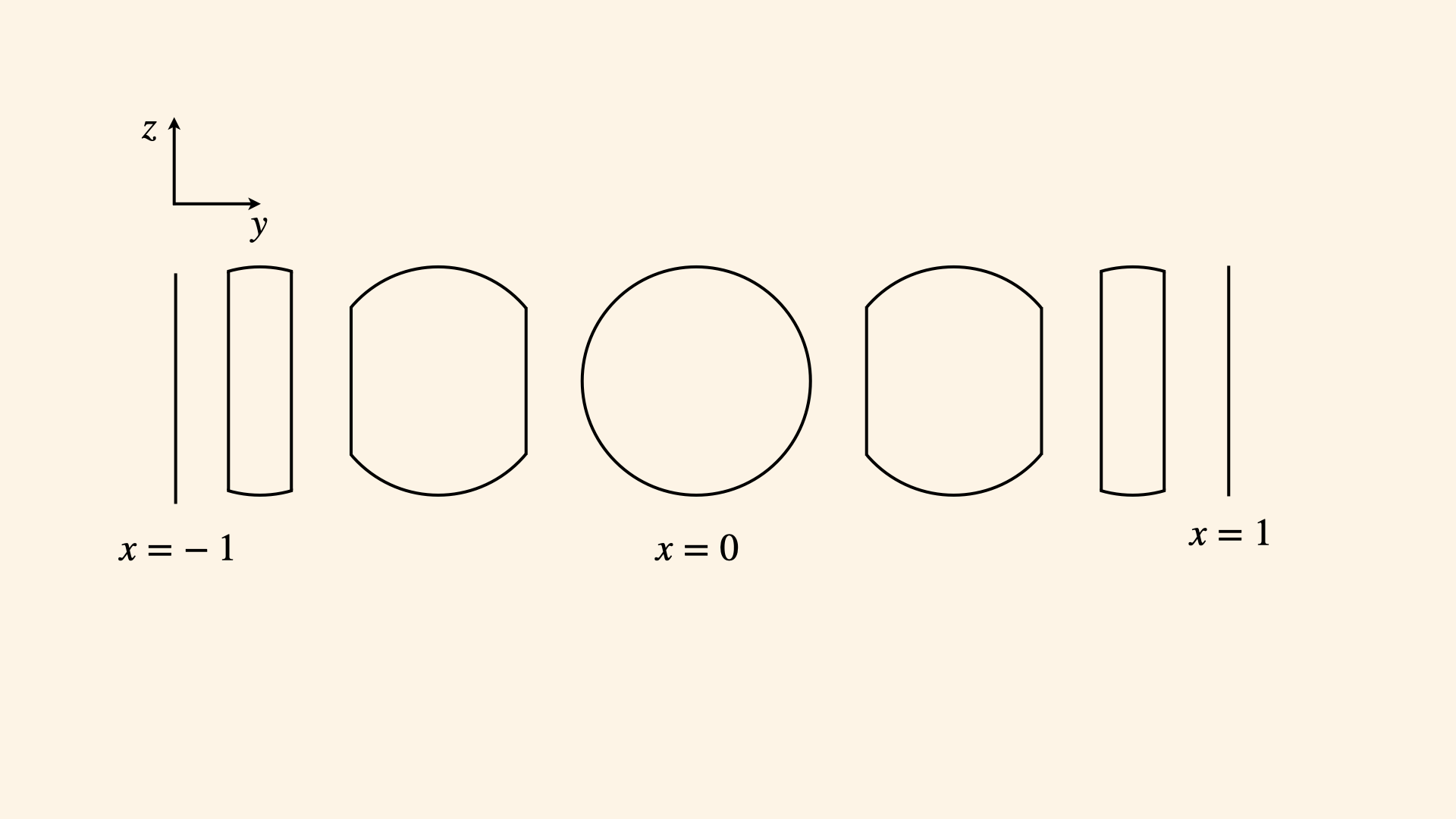Since the intersections are continuously changing shape from line to a full circle and back, we must set up an integral to evaluate the infinite sum of these infinitely thin discs whose shape changes as we move through the cylinder. Recall that a volume integral is nothing more than a sum over a certain space of infinitesimal cubes $dV = dx\cdot dy \cdot dz$. To set it up, we must tell it the right limits for the three axis, which defines the shape of the volume we are computing. The integral will look something like: $$V = \int_{x_min}^{x_max}\int_{y_min}^{y_max} \int_{z_min}^{z_max} dz dy dx$$Let's go axis by axis. We've already said that in the x axis we are counting the circular discs slicing the cylinder from $x_min=-1$ to $x_max=1$. Note there's nothing special about the way we've set up our coordinate system, i.e. we could be moving x from 4 to 6 so long as the distance between the two points is 2 - diameter of the circle. Next, notice that every time we take another slice along th x axis, the width in the y axis direction changes, going from 0 to circle diameter (2) and back to 0. This width is each time bounded by the circle of radius in the x-y plane - namely, the face of the cylinder we are cutting through.

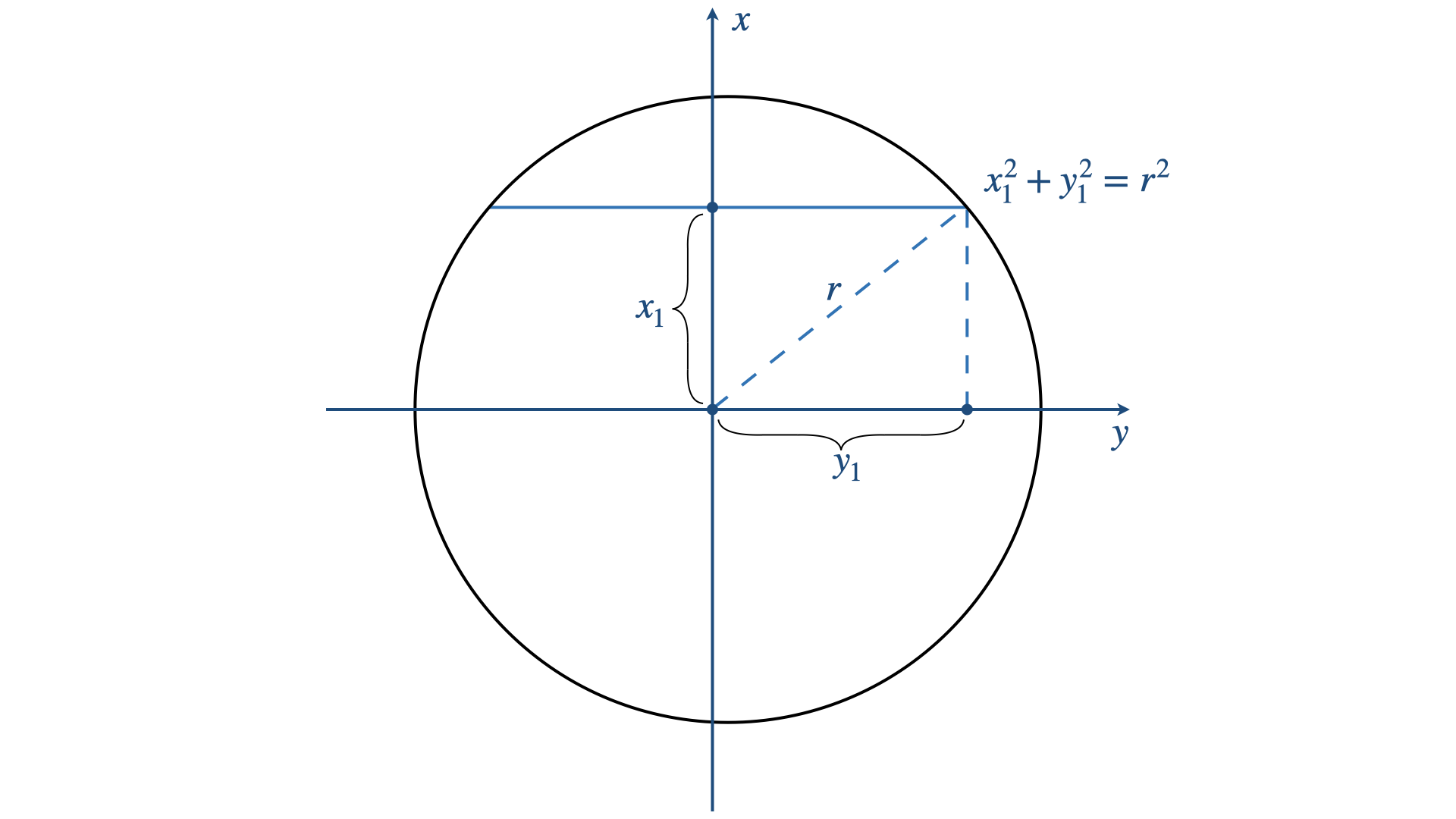Zooming in on this circle, we see that each time we take a slice (e.g. $x_1$), the width of the intersection along the y axis is bounded by the circle from $y_min=-\sqrt{1-x_1^2}$ to $y_max=+\sqrt{1-x_1^2}$. This comes from the circle equation, whereby for any points $x_1$ and $y_1$ along the circle of radius $r$, the relationship $x_1^2+y_1^2=r^2$ holds.

Okay, now we have our $x$ and $y$ bounds - and we have $z$ axis bounds left. Looking again at the second image, you see that the z-axis height varies for each intersection as we move along the y axis. For instance, looking again at the intermediate cut, we see that as we move along the y-axis width we just defined, its z-axis height is bound by a circle of radius 1 in the y-z plane (corresponding to the face of the cylinder we split into discs and are using to slice the other cylinder).

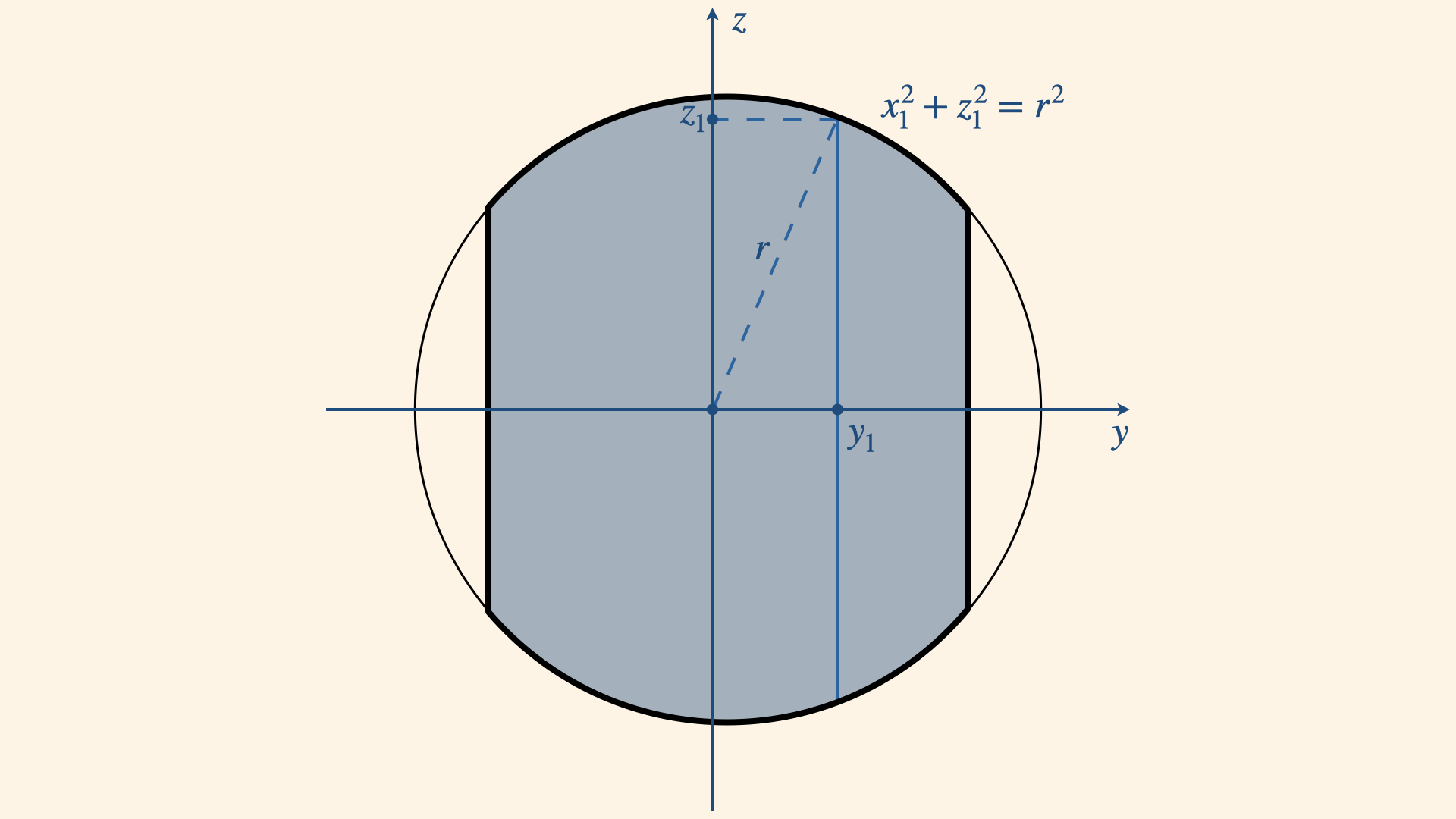Therefore once we know the $y_min$ and $y_max$ we are moving between for a given $x$-axis cut, we define $z$-axis limits as a function of the $y1$ position as $y_min=-\sqrt{1-y_1^2}$ and $y_max=+\sqrt{1-y_1^2}$. Once again we are using the circle of radius 1 equation to relate the y axis position and z axis limits. Putting this all together, we have an integral as follows: $$V=\int_{-1}^1 \int_{-\sqrt{1-x^2}}^{+\sqrt{1-x^2}} \int_{-\sqrt{1-y^2}}^{+\sqrt{1-y^2}}dz dy dx$$ One last complication is that this integral is quite difficult to evaluate. To make it easier we will just swap the limits of the first two integrals. Look a them again: in the x-axis we are moving between -1 and 1 and in the y-axis we are moving bottom to top bound by the circle. This is the same as moving between -1 and 1 in the y-axis and moving left to right bound by the circle in the x-direction. Therefore we can re-write the integral as: $$V = \int_{-1}^{+1}\int_{-\sqrt{1-y^2}}^{+\sqrt{1-y^2}}\int_{-\sqrt{1-y^2}}^{+\sqrt{1-y^2}}dz dx dy$$ Now this is way easier to evaluate, as we have the same limits for the two inner integrals: $$V=\int_{-1}^{+1}\int_{-\sqrt{1-y^2}}^{+\sqrt{1-y^2}}2\sqrt{1-y^2}dx dy=$$ $$\int_{-1}^{+1}4(1-y^2)dy=$$ $$8\left[y-\frac{y^3}{3}\right]^{+1}_{-1}=\frac{16}{3}$$That's our answer, $\frac{16}{3}$.