Answer

When asked for your optimal (bidding) strategy, start by evaluating the expected payoffs of different strategies. Our strategy here means chosing a bid $b$, so we need the expected payoff we get by bidding an amount $b$.

To get the expected payoff, we fix b and find the different possible payoffs and their probabilities. Let's denote the true value of the chest as $V$. We know that if $b\geq V$ - we win $1.5V-b$ (as we pay $b$ to buy it and sell it to our friend at $1.5V$), whereas if $b\lt V$, we get 0. Now that we know the payoffs, we need the probabilities that $b\geq V$ or $b\lt V$. We know that $V$ is anywhere between 0 and 400, so we can safely assume a uniform distribution between 0 and 400 (i.e. all values in the range are equally likely). So for a chosen $b\in[0,400]$, the chance that $V\leq b$ is simply $\frac{b}{400}$, and chance that $V\gt b$ is $\frac{400-b}{400}$. Putting all this together, once we chose our bid $b$, our payoff is: $$\text{Payoff}=\frac{b}{400}\left(1.5 \cdot V - b\right)$$And since $V$ is not known, we will find our optimal strategy as the $b$ which maximises the expected payoff. So, assuming we chose a $b$, the expected payoff is: $$E(\text{Payoff | b})=\frac{b}{400}\left(1.5 E(\text{V|b})-b \right)$$Now $V$ value doesn't depend on our bid, so $E(\text{V | b})=E(V)$. Since we assumed $V$ was a uniform random variable, its expected value is simply the midpoint between 0 and 400, i.e. 200. So expected payoff becomes $\frac{b}{400} \left(300-b\right)$.

Now let's first check if the game is worth playing at all, i.e. if this payoff is ever above 0. We see this happens when $b$ is positive and below 300. To convince yourself, you can sketch the function as below: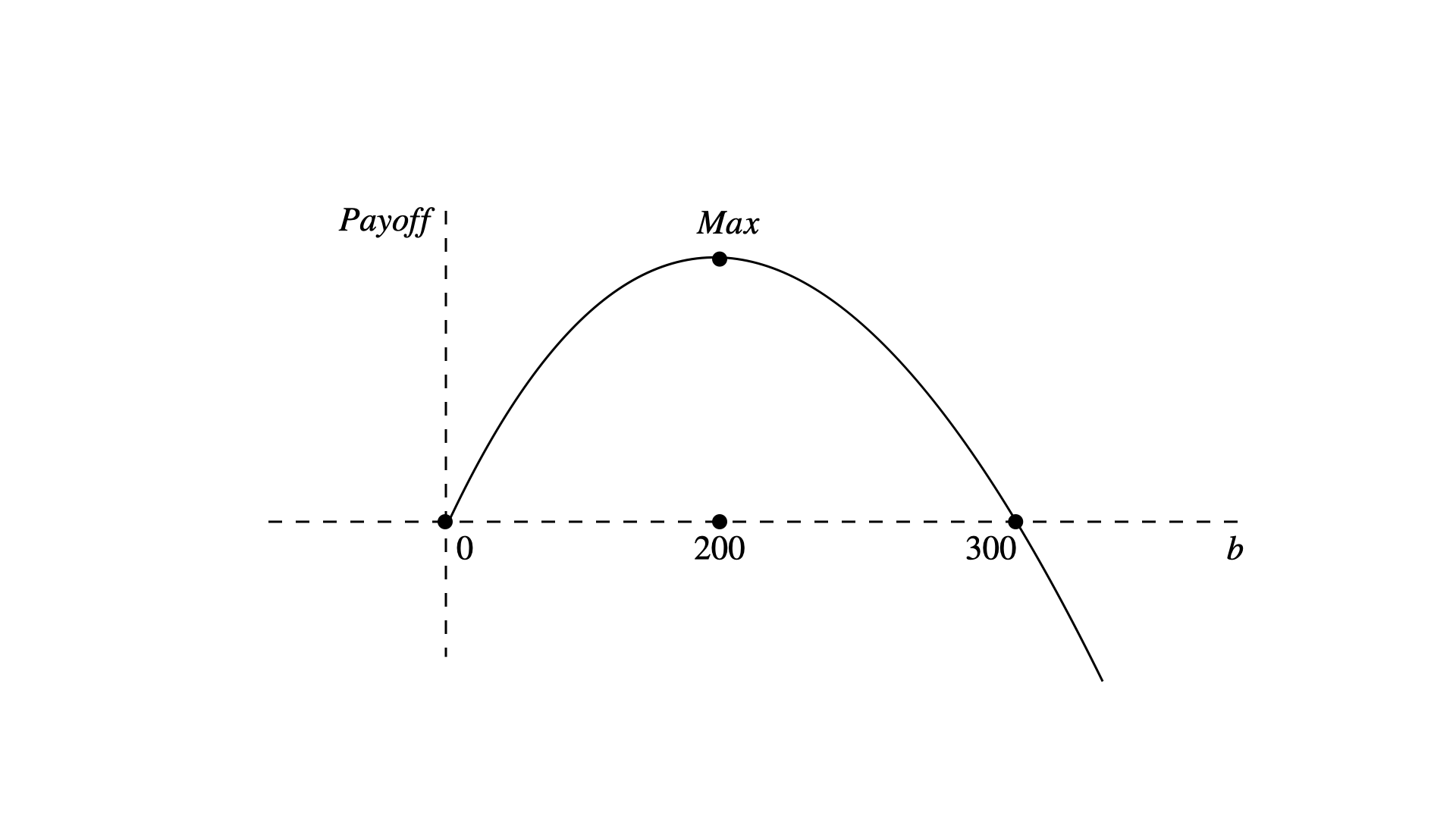 Then, our optimal $b$ should be the one that leads to the highest possible expected payoff. We can already see graphically that this is the midpoint between the two roots of the quadratic functions, i.e. 150. Otherwise, we can set the derivative of the payoff function to 0: $300-2b=0$ to find the optimal $b=150$. In conclusion, our optimal strategy is to bid 150 for the treasure chest.